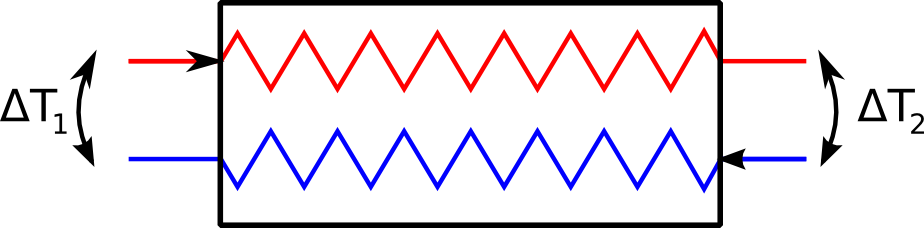
A robust expression for the Log Mean Temperature Difference (LMTD)

The Log Mean Temperature Difference (LMTD) is a deceivingly simple expression to compute the average driving force in heat transfer:

LMTD = (ΔT1 - ΔT2) / log(ΔT1 / ΔT2);

The ΔT1 and ΔT2 are the temperature approaches, as in this figure:

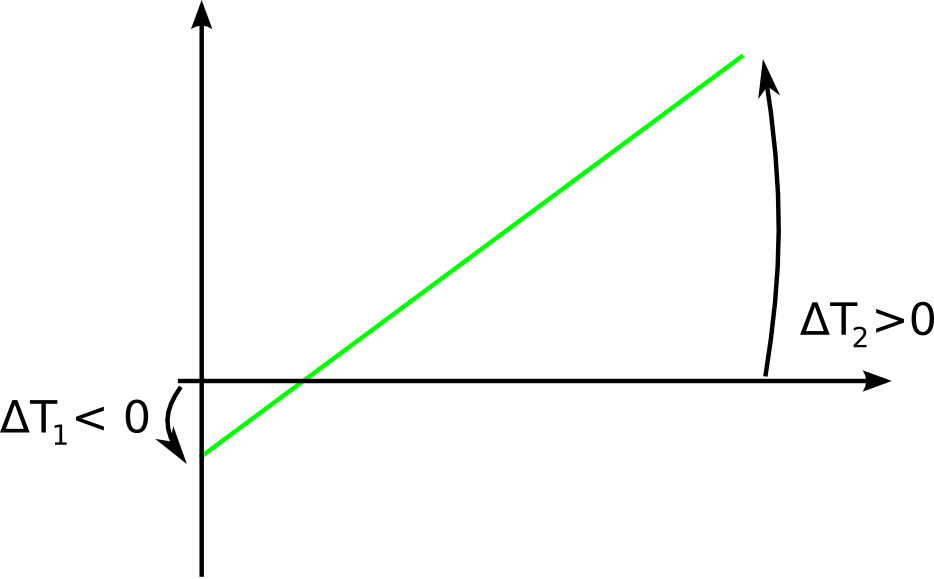
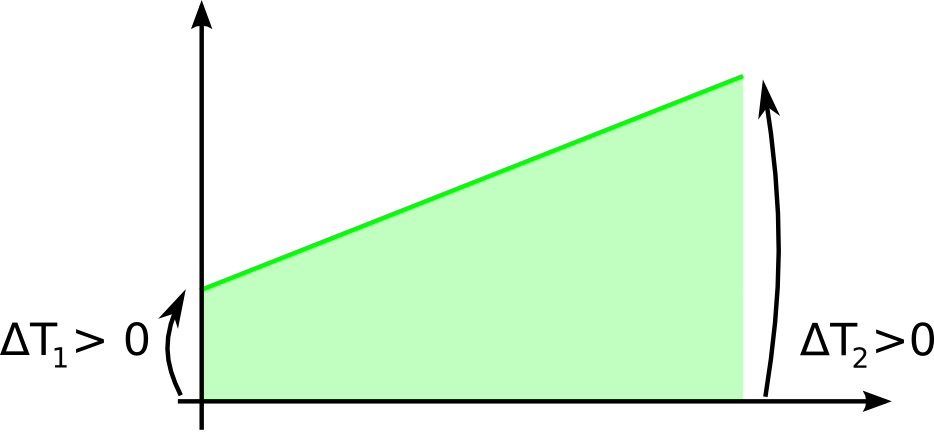
Everything works well when the approaches are both non-zero, different in value and have the same sign, as in these two figures:

But when this expression is applied in practice, it may become singular whenever:

1. The denominator equals zero, because the two temperature approaches are the same (this is a purely accidental singularity, because the mathematical limit of the above expression exists and is equal to the temperature approaches)
2. The argument of the logarithm function is zero, because ΔT1 = 0
3. The argument of the logarithm function is infinity, because ΔT2 = 0
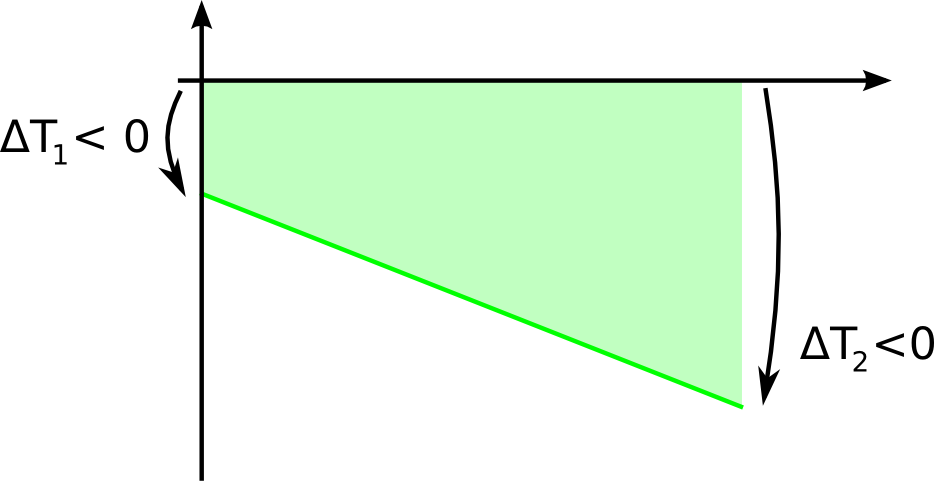
4. The argument of the logarithm function is negative, because the sign of ΔT1 and of ΔT2 are different, as is the next figure:

The fact that the LMTD expression screws up if any one of the temperature approaches is equal to zero is reasonable, because an infinite heat transfer area would be required. The fact that it screws up if the sign of the temperature approaches are different indicates that the LMTD is designed to calculate heat transfer in only one direction.
Singularities are often encountered if some iterative algorithm which encapsulates the heat transfer calculation enters a non-feasible region of the solution search space, and generates unphysical values for the temperature approaches.
In this case the expression above returns #NaN or #Inf and the errors may screw up completely the iterative algorithm, preventing it to ever get back in the feasible region and even less getting to the actual solution.

It would be therefore helpful to reformulate the LMTD expression so that it is more robust and gives reasonable if not correct results even for unfeasible input parameters. The modified LMTD expression should satisfy three requirements:

1. to return the same result as the conventional expression when the approaches have reasonable values
2. to not violate the second principle of thermodynamic, whereby no heat can be transferred from a colder body to a hotter body.
3. to avoid sharp discontinuities that are harmful to numerical algorithms.

The method to stabilize the LMTD expression we have tested within LIBPF is based on a dead band, i.e. a range of small temperature approaches (lower in absolute value than a certain threshold). We assume that if anywhere along the heat exchanger we are getting a local temperature difference lower than the threshold in absolute value, we can assume that heat transfer is negligible in the affected fraction of the area.
So if one of the approaches is getting close to zero, it is clipped to the threshold value; furthermore the effective area is reduced by a factor, such that the part of the area where the local temperature difference is lower than the threshold does not contribute to the transfer; this reduction is computed assuming a linear temperature profile.

The method when applied to the case of sign reversal above is represented in this figure, where the dead band is painted in darker yellow color: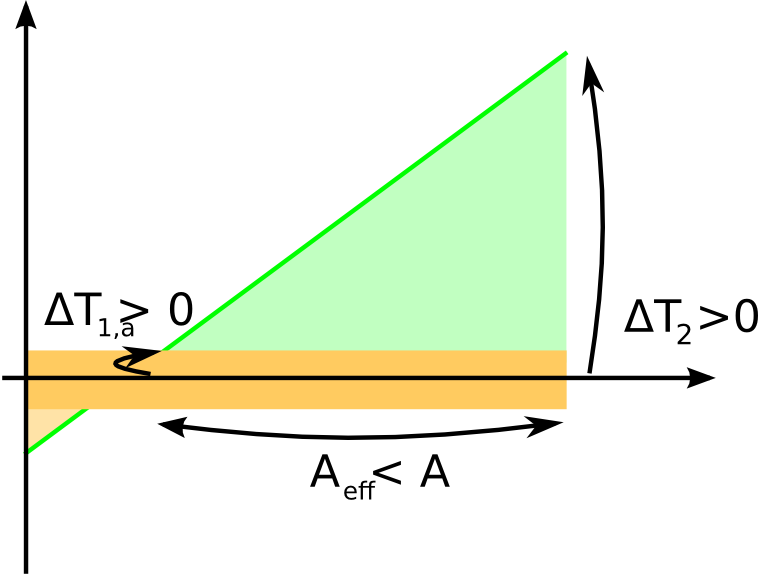The part of the area where the sign is opposite to the dominating heat transfer direction (light yellow region) is not considered at all, i.e. no heat is transferred back. In other words, the direction of the heat transferred is set by the sign of the approach larger in absolute value.

The resulting pseudo code is:

if (abs(ΔT1) <= deadBand) {
  if (abs(ΔT2) <= deadBand) {
    LMTD = (ΔT1 + ΔT2) / 2.0;
  } else {
    ΔT1clip = deadBand*ΔT2/abs(ΔT2); // absolute value is set to deadBand, sign is the same as ΔT2
    LMTD = ((ΔT1clip - ΔT2) / (ΔT1 - ΔT2)) * (ΔT1clip - ΔT2) / log(ΔT1clip / ΔT2);
  }
} else if (abs(ΔT2) <= deadBand) {
  ΔT2clip = deadBand*ΔT1/abs(ΔT1);
  LMTD = ((ΔT1 - ΔT2clip) / (ΔT1 - ΔT2)) * (ΔT1 - ΔT2clip) / log(ΔT1 / ΔT2clip);
} else if ((ΔT1 * ΔT2) <= 0.0) {
  if (abs(ΔT1) <= abs(ΔT2)) {
    ΔT1clip = deadBand*ΔT2/abs(ΔT2);
    LMTD = ((ΔT1clip - ΔT2) / (ΔT1 - ΔT2)) * (ΔT1clip - ΔT2) / log(ΔT1clip / ΔT2);
  } else {
    ΔT2clip = deadBand*ΔT1/abs(ΔT1);
    LMTD = ((ΔT1 - ΔT2clip) / (ΔT1 - ΔT2)) * (ΔT1 - ΔT2clip) / log(ΔT1 / ΔT2clip);
   }
 } else {
   LMTD = (ΔT1 - ΔT2) / log(ΔT1 / ΔT2);
 }